Uwielbiamy statystki, chociaż jak mówił Mark Twain „są trzy rodzaje kłamstw: kłamstwa, bezczelne kłamstwa i statystyki”. A w tych ostatnich możemy spotkać bohatera dzisiejszego wpisu, czyli Paradoks Simpsona.
Wiemy, że nasza intuicja często nas zawodzi i jesteśmy podatni na rozmaite błędy poznawcze. Niektórzy z tych powodów uciekają w stronę twardych liczb. Liczby nie mogą się przecież mylić, prawda?
Paradoks Simpsona
Paradoks Simpsona to jeden z fenomenów w statystyce. Czasami analizując dane w grupach otrzymamy zupełnie inne informacje o trendach, niż analizując je całościowo! W zależności od tego, jak pokroimy dane, możemy pokazać zupełnie coś innego.
Brzmi niewiarygodnie? Ten „paradoks” związany jest z licznością elementów w podgrupach. Im mniej elementów w badanej grupie, tym łatwiej o zaburzenia wyników. Mówi o tym chociażby prawo małych liczb.
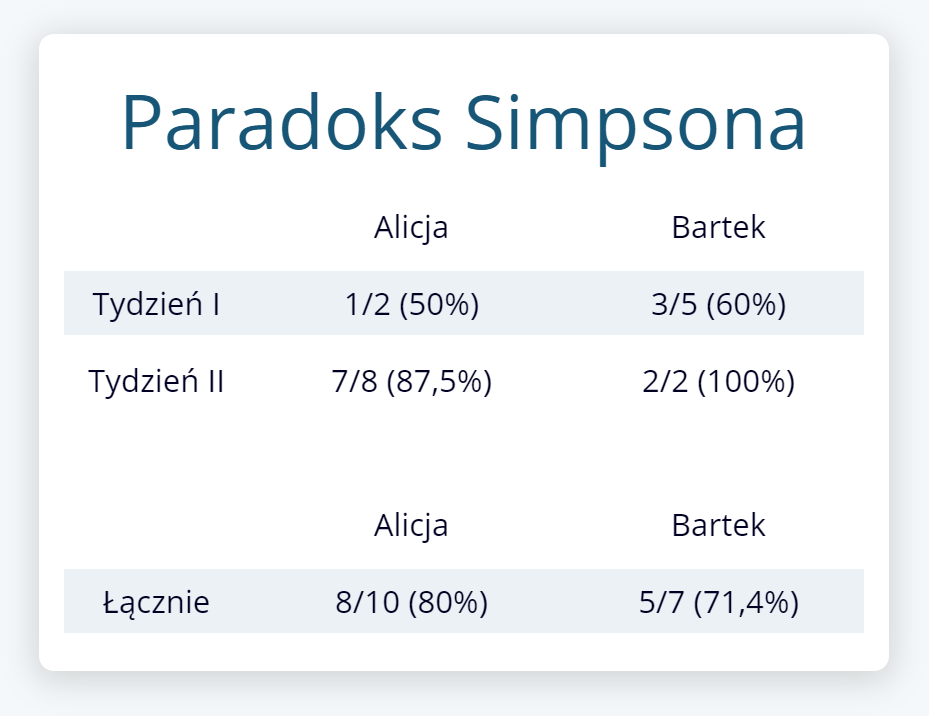
Przyjmijmy, że Alicja i Bartek przez dwa tygodnie poprawiają błędy. W pierwszym tygodniu Alicja poprawiła 1 z 2 błędów, a w drugim 7 z 8. Dla Bartka te liczby to odpowiednio 3 na 5 i 2 na 2.
Może się wydawać, że Bartek ma lepszą skuteczność poprawy błędów. W pierwszym tygodniu poprawił 60% błędów (kontra 50% Alicji), a w drugim 100% (kontra 87,5% Alicji) – za każdym razem, w ujęciu tygodniowym jest lepszy niż Alicja.
Ale to przecież ona przez dwa tygodnie poprawiła 8/10 swoich błędów (80%), a Bartek jedynie 5/7 (71,4%)!
Gdzie znajdziemy Paradoks Simpsona?
Jednym z bardziej znanych przypadków wystąpienia Paradoksu Simpsona były oskarżenia płynące pod adresem University of California w Berkeley w Stanach Zjednoczonych o faworyzowanie mężczyzn. Dla przykładu, w 1973 roku z 8442 mężczyzn przyjęto „aż” 44%, a z 4321 kobiet „zaledwie” 35%.
Pojawiły się oskarżenia o jawną dyskryminację kobiet. Gdy jednak przeanalizowano odsetek przyjmowanych kobiet i mężczyzn w poszczególnych departamentach, okazało się, że w większości z nich to kobiety były faworyzowane! Po prostu mężczyzn nie tylko było więcej, ale też aplikowali do bardziej obleganych departamentów. Więcej ich odrzucano, ale też i sumarycznie – więcej ich przyjęto.
Nie wystarczy z radością krzyknąć „A jest większe od B”, jeżeli nie wiemy z czego wynika ta różnica. Jeśli grupa A zawiera 90 elementów o cesze X i 10 o ceszeY, a B – odwrotnie, to być może nie powinniśmy w ogóle patrzeć na cechy A i B, ale na X i Y?
Pozostając w Stanach – w ostatnich latach ustandaryzowane wyniki testów ośmioklasistów w Wisconsin były wyższe od wyników uczniów w Teksasie. Np. w 2015 roku było to 159 kontra 156, a w 2011 różnica wyniosła aż 6 punktów (odpowiednio 159 i 153). Czyżby w Teksasie były gorsze szkoły?
Gdy rozbito te wyniki na grupy społeczne, okazało się, że w każdej z nich to Teksańczycy byli górą. Po prostu w Wisconsin jest mniej przedstawicieli grup, które z różnych powodów radzą sobie gorzej. Problem wynikał z demografii, a nie z jakości nauczania.
To jak w końcu analizować dane?
Problemem nie są statystyki, ale interpretacja. Liczby, procenty, średnie, wariancje, współczynniki i tak dalej to tylko suche liczby. Paradoks Simpsona zwraca nam uwagę na przedmiot naszych badań. Nie analizujemy liczb dla samej li tylko radości z analizy. Coś przecież mierzymy, chcemy potwierdzić jakąś tezę.
Z pomocą przychodzi nam nie tylko dokładniejsza analiza (np. rozbicie na grupy), ale i wizualizacja – bo nasze dość ograniczone umysły często nie są w stanie objąć abstrakcyjnych danych. I tak typowa graficzna reprezentacja paradoksu Simpsona to dwa podobne trendy w dwóch rozłącznych grupach.
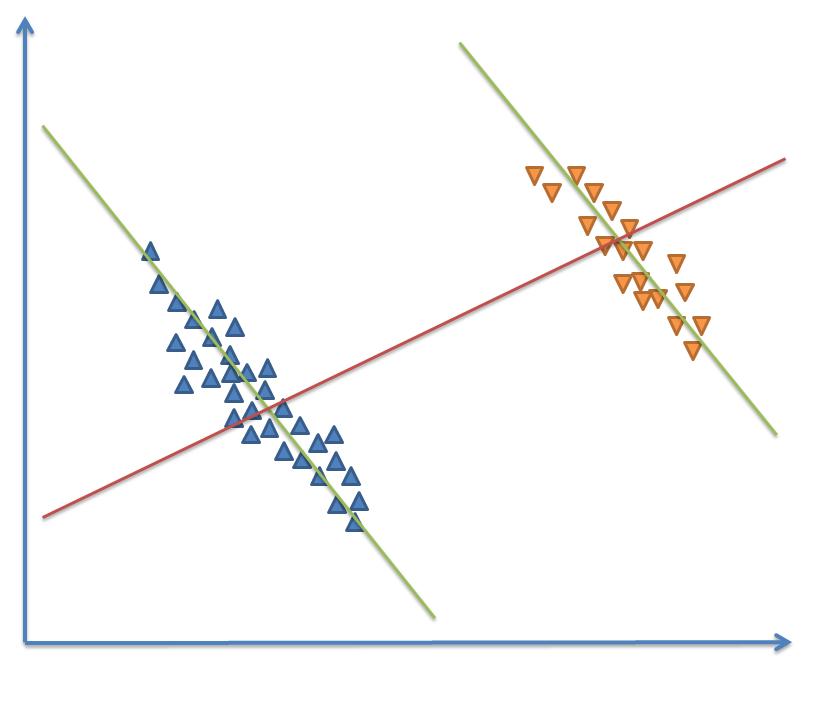
Analizując je oddzielnie możemy powiedzieć, że współczynnik korelacji jest ujemny (zielone linie). Patrząc na całość danych – korelacja jest dodatnia (linia czerwona).
W teorii jest to panaceum na paradoks Simpsona, ale problemem jest oczywiście dobór grup. Jeżeli nie wiemy, co powoduje aż takie różnice, to nie wiemy też jak dobrać próbki i jakie cechy wziąć pod uwagę, żeby zobaczyć różnice. Skąd mamy wpaść na to, która to cecha powoduje „paradoks”? A może to wszystko tylko wynik przypadku i nie ma co poświęcać na to czasu?
Kwartet Anscombe’a
W 1973 statystyk Francis Anscombe zaprezentował cztery zestawy danych o dokładnie takich samych cechach. Takie parametry jak średnia arytmetyczna, wariancja, współczynnik korelacji czy równanie regresji liniowej są identyczne dla każdego z nich. Nie byłoby w tym nic dziwnego, gdyby nie fakt, że te cztery zestawy danych miały zupełnie inną reprezentację graficzną.
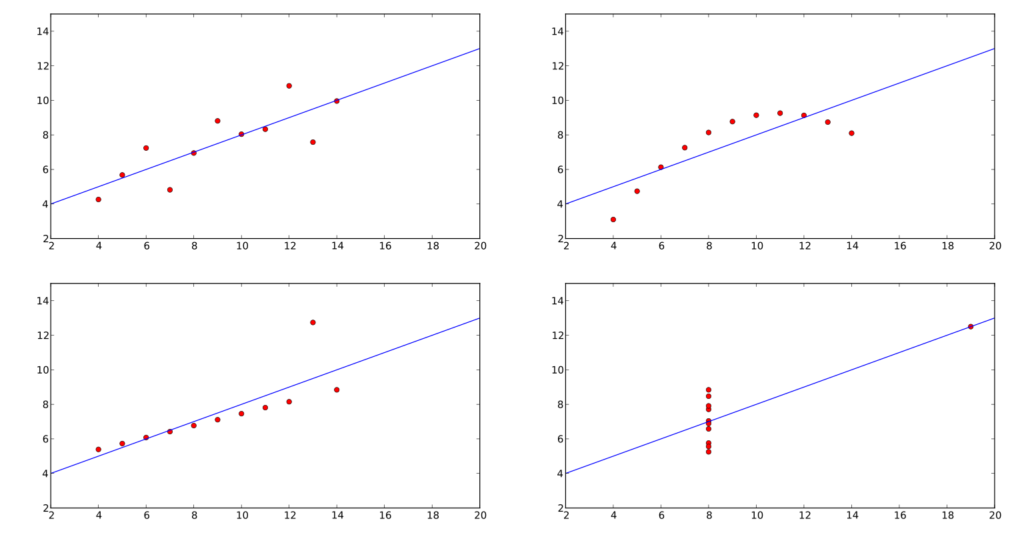
Każdy zestaw danych sugeruje inną zależność pomiędzy dwoma zmiennymi. W niektórych wyraźnie widać jak jeden wyjątek (Czarny Łabędź) wpływa na regresję liniową. Wszystkie z nich dobitnie pokazują, że nie możemy opierać się wyłącznie na analizie numerycznej oraz musimy zwracać szczególną uwagę na pojedyncze odstępstwa i błędy w zbieraniu danych.
Czy wyjątek, który znaleźliśmy tylko raz jest błędem w obliczeniach, nieścisłością w badaniu czy Czarnym Łabędziem, którego nijak nie możemy potwierdzić, bo nie wiemy, kiedy wydarzy się następny? Takie myślenie zaprowadzi nas albo do paranoi (lepiej nie), albo do bardzo ostrożnego posługiwania się statystykami i bardzo dokładnej ich analizy (oby).
Och, ta statystyka
Nie możemy rozpatrywać jakichkolwiek statystyk w oderwaniu od rzeczywistości. Jeśli badamy efektywność zespołów, to musimy wziąć pod uwagę nieobecności, rodzaj zadań i zależności pomiędzy nimi, względne i bezwzględne obciążenie, itd.
Nie można powiedzieć „efektywność spadła, musimy coś z tym zrobić”. Dlaczego spadła? A może gdyby nie nasze działania, to byłoby jeszcze gorzej? A może, niestety, gdybyśmy nic nie robili, to byłoby lepiej?
Uwzględnianie tylko i wyłącznie jednej zmiennej, to proszenie się o kłopoty. Myśląc w ten sposób Ferrari to strasznie słaby, bo drogi, samochód.
Paradoks Simpsona pokazuje, że bezpodstawne łączenie różnych grup w celach analizy statystycznej może prowadzić do złych wyników, podobnie jak analizowanie ich oddzielnie. Nie wiemy, która interpretacja jest poprawna, jeśli potraktujemy sprawę po łebkach.
A przecież robimy to cały czas – analizujemy hurtowo błędy w interfejsach, aplikacji i hurtowniach danych, patrzymy na efektywność bez uwzględnienia rodzaju zadań czy doświadczenia osób, czy też np. przepisujemy „metodykę agile” jako panaceum na problemy z kosztami.
Kontekst jest ważny. Zarówno przy wprowadzaniu metodyk zwinnych, analizie błędów czy ocenie opłacalności jakiegoś rozwiązania. Szczególnie ważny wydaje się być przy naszym dzisiejszym temacie – analizie statystycznej. A tam czyha na nas nie tylko Paradoks Simpsona…
